特征降维算法总结比较

特征降维有利于减少描述分为特征提取与特征的选择.这两者是有区别的
特征提取指对特征进行某种变换,得到新特征; 特征选择指通过某些方法获取特征的子集. 这篇文章是对以上两者的总结.

1 特征提取 (Feature extration)
2 特征选择 (Feature selection)

1 特征提取(Feature extration)

特征提取指通过特征组合的方式生成新特征的过程.这个组合可以是线性的(如,PCA),也可以是非线性的(如,PCA的非线性推广:KPCA)

1.1 主成分分析 (Principal Component Analysis, PCA)

1.2 核主成分分析 (Kernel Principal Component Analysis, KPCA)

1.3 线性判别分析 (LDA)

LDA与PCA最大的差别在于:PCA是无监督的,而LDA是有监督的; PCA着重描述特征,而LDA着重抓住其判别特征; 因此PCA变换矩阵是正交的,而LDA一般不是正交的(并不关注).

线性判别分析的核心思想
通过线性变换,使得变换后的矩阵对应的,不同类别的样本尽可能地分开.
什么叫尽可能分开呢?可以从两个方面来衡量.
1. 各类样本的类间方差尽可能大.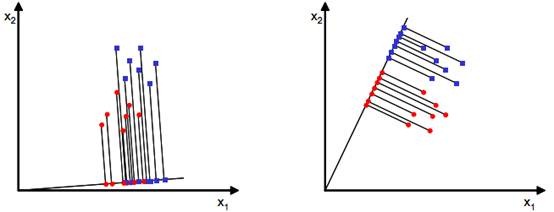

右方两类的样本中心较左方相隔更远,因此分类效果更好.

2. 各类样本的类内方差尽可能小.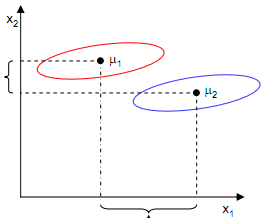

光考虑类间中心距离还是不够的.从上图可以看到,若投影到x1上,虽然两类中心相比投影到x2上,相隔较远.但由于两类在x1上的方差都很大,因此从分类角度看,效果比不上投影到x2上.

因此,必须同时考虑以上两方面才能达到我们想要的效果.
看,这其实就是方差分析的思想. 因此目标函数可以取统计意义上的F值.F值越大越好.
目标优化函数
接下来我们要想,怎么量化这两个标准.
原始特征矩阵 $X_{p \times n}$ ;
转换矩阵 $W_{p \times d}$ ;
线性变换后的新矩阵 $Y_{d \times n} = {W}'_{p \times d}\cdot X_{p \times n}$ .
其中,
n为样本数, p为特征数, d为变换后的特征数.
- 使变换后各类样本的类间方差尽可能大.
  变换后的各类样本中心:
  $\widetilde{\mu_{j}} = \frac{1}{n_{j}}\sum_{y \in \omega _{j}} y$
  其中,
  $\omega _{j}$ 指第j类； $n_{j}$ 指第j类的样本数.
  
  变换后的总体样本中心:
  $\widetilde{\mu}=\frac{1}{n}\sum_{i=1}^{n}y_{i}=\frac{1}{n}\sum_{i=1}^{n}w_{i}\cdot X$
  
  因此,变换后样本类间协方差矩阵 (Between-Class Scatter Matrix)可表示为:
  $\widetilde{S_{b}}=\sum _{j=1}^{c}\frac{n_{j}}{n}(\widetilde{\mu_{j}}-\widetilde{\mu})(\widetilde{\mu_{j}}-\widetilde{\mu})'$
  显然,这是一个 $d \times d$ 维的矩阵.
- 使变换各类样本的类内方差尽可能小.
  样本类内协方差矩阵 (Within-Class Scatter Matrix)可表示为:
  $\widetilde{S_{w}}=\sum _{j=1}^{c}\sum_{y \in \omega _{j}} (y-\widetilde{\mu_{j}})(y-\widetilde{\mu_{j}})'$
- 目标函数
  $J(W) = \frac{\widetilde{S_{b}}}{\widetilde{S_{w}}}$
- 目标函数的展开
  可以看到,我们现在的目标函数是由线行变换后的Y出发推出来的.我们更希望计算时能从X出发,因此,我们把 $Y=W'X$ 代入目标函数.
  可得:
  1. $\widetilde{\mu} = W'\mu$
  $\begin{align*} proof: \\ \widetilde{\mu} &= \frac{1}{n}\sum_{i=1}^{n} y_{i} &=\frac{1}{n}\sum_{i=1}^{n} W'x_{i} &=W'\cdot \frac{1}{n}\sum_{i=1}^{n} x_{i} &=W'\mu \end{align*}$
  
  2. $\widetilde{\mu_{j}} = W'\mu_{j}$
  $\begin{align*} proof: \\ \widetilde{\mu_{j}} &= \frac{1}{n_{j}}\sum_{y \in \omega _{j}} y &=\frac{1}{n_{j}}\sum_{x \in \omega _{j}}W'x &=W'\cdot \frac{1}{n_{j}}\sum_{x \in \omega _{j}}x &=W'\mu_{j} \end{align*}$
  
  3. $\widetilde{S_{b}} = W'S_{b}W'$ , 其中, $S_{b}$ 为原样本类间协方差矩阵
  $\begin{align*} proof: \\ \widetilde{S_{b}}&=\sum _{j=1}^{c}\frac{n_{j}}{n}(\widetilde{\mu_{j}}-\widetilde{\mu})(\widetilde{\mu_{j}}-\widetilde{\mu})'\\ &=\sum _{j=1}^{c}\frac{n_{j}}{n}(W'\mu_{j}-W'\mu)(W'\mu_{j}-W'\mu)'\\ &=W'[\sum _{j=1}^{c}\frac{n_{j}}{n}(\mu_{j}-\mu)(\mu_{j}-\mu)']W\\ &=W'S_{b}W \end{align*}$
  
  4. $\widetilde{S_{w}} = W'S_{w}W$ , 其中, $S_{w}$ 为原样本类内协方差矩阵
  $\begin{align*} proof: \\ \widetilde{S_{w}}&=\sum _{j=1}^{c}\sum_{y \in \omega _{j}} (y-\widetilde{\mu_{j}})(y-\widetilde{\mu_{j}})'\\ &=\sum _{j=1}^{c}\sum_{x \in \omega _{j}} (W'x-W'\mu_{j})(W'x-W'\mu_{j})'\\ &=W'[\sum _{j=1}^{c}\sum_{x \in \omega _{j}} (x-\mu_{j})(x-\mu_{j})']W\\ &=W'S_{w}W \end{align*}$
  
  5. 易得最终的目标优化函数:
  $J(W) = \frac{W'S_{b}W}{W'S_{w}W}$ .该值越大越好.
目标优化函数求解
我们有了目标函数 $J(W)$ ,接下来我们需要对其进行求解.
注意到,对变换矩阵W扩大C倍(C>0),方向没有改变.
因此我们可以只考虑 $W'S_{w}W=1}$ 时的情况,即对目标函数添加了一个条件.

这里大家可能会疑惑.上面不是说过, $\widetilde{S_{b}}$ 是一个 $d \times d$ 维的矩阵吗? 怎么可以将它设为常数1呢?
这是因为,我们希望能按判别能力从大到小依次找出W的每一维向量.那么取前d维就可以组成最终的变换矩阵W啦.(这有一丢丢类似PCA)
因此,在求解时,我们将W设置为 $1 \times p$ 的向量,那相应的,得到的 $\widetilde{S_{b}}$ , $\widetilde{S_{w}}$ 都将是一个常数

现在我们的目标函数变成了:
$W = argmax\ W'S_{b}W\\ s.t.\ W'S_{w}W=1$

利用拉格朗日乘子,将条件与目标函数合并到一起,得到:
$C(W)=W'S_{b}W-\lambda (W'S_{w}W-1)$
这显然是一个上凹函数,有且只有一个极大值.
因此,求偏导并令其为0:
$\Rightarrow \frac{\partial C(W)}{\partial W}=2S_{b}W-2\lambda S_{w}W=0$
$\Rightarrow S_{b}W=\lambda S_{w}W$
若 $S_{w}$ 非奇异,即其逆存在,则有:
$\Rightarrow (S_{w}^{-1}S_{b})W=\lambda W$

看到了吧, $\lambda$ 是 $(S_{w}^{-1}S_{b})$ 的特征值;W是对应的特征向量. 因此,第i大的特征根对应的特征向量,就是W的第i个分量.取前d个特征向量合并,得到的就是W.

这里要注意的是, $S_{w}$ 非奇异这个条件不一定成立,在实用中往往先对原特征矩阵做一次PCA,再做LDA.

梁耀荣

特征降维算法总结比较

1 特征提取(Feature extration)

1.1 主成分分析 (Principal Component Analysis, PCA)

1.2 核主成分分析 (Kernel Principal Component Analysis, KPCA)

1.3 线性判别分析 (LDA)

1.4 局部线性嵌入 (LLE)